(v) lim x→2+ g(x)

Question

Let

g(x) =	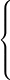x		if x < 1
6		if x = 1
2 − x2		if 1 < x ≤ 2
x − 5		if x > 2

.

(a)

Evaluate each of the following, if it exists. (If an answer does not exist, enter DNE.)

(i)

lim x→1⁻ g(x)

 

(ii)

lim x→1 g(x)

 

(iii)

g(1)

 

(iv)

lim x→2⁻ g(x)

 

(v)

lim x→2⁺ g(x)

 

(vi)

lim x→2 g(x)

 

Answer 1

For this piecewise-defined function, we need to look at what value x is approaching and from which side, in order to determine which function rule to use and therefore determine the limit.

)

i) lim x→ 1^- means x less than 1 so g(x) = x and lim_x→1^- g(x) = 1

ii) lim_x→1 g(x) DNE since the right-handed limit = 6 which ≠ 1, the left-handed limit calculated above.

iii) g(1) = 6

iv) lim_x→2^- means x less than 2 so g(x) = 2 - x² and lim_x→2^- g(x) = -2

v) lim_x→2⁺ means x greater than 2 so g(x) = x - 5 and lim_x→2⁺ g(x) = -3

vi) similarly to our answer to ii), because the 2 answers to iv) and v) disagree, lim_x→2 g(x) DNE.