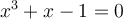Calculus need help please

Question

8. Using the Mean Value Theorem and Rolle’s Theorem, show that has exactly one real root.

Answer 1

We use the Mean Value Theorem to show that there is at least one real root,

and use the Rolle's Theorem to show that there cannot be more than one.

Both theorems apply to functions that are continuous and differentiable on a particular interval.

The function f(x) = x³ + x - 1, being a polynomial, is both continuous and

differentiable on (-∞, +∞), making both theorems applicable.

1) Proof that f(x) has at least one root:

There are values where f is positive, and there are values where f is negative.

For example

f(-1) = -3, f(1) = 1

By Mean Value Theorem there exists r ∈ (-1, 1) such that f(r) = 0.

2) Proof that f(x) has no more than one root:

Suppose the contrary and we will derive a contradiction.

Assume there exist real values r₁ < r₂ such that f(r₁) = f(r₂) = 0.

By Rolle's Theorem there exists r₀ ∈ (r₁, r₂) such that f'(r₀) = 0.

But

f'(x) = 3x² + 1

which is > 0 for all x, which contradicts the existence of r₀,

which proves the statement.