
1 Expert Answer
Daniel B. answered • 05/19/21
A retired computer professional to teach math, physics
This looks like a trick question because f(x) never attains a global maximum.
Notice that f(x) -> ∞ as x -> ∞.
But let's go through the motions.
First lets calculate the fist and second derivative:
f'(x) = 1 + 2x/(x²-1)
f"(x) = 2/(x²-1) - 4x²/(x²-1)²
In general, a function attains its maximum value at a critical point, or at a boundary
of its domain.
The domain of our function f(x) is the set of x making the argument on ln() positive:
x² - 1 > 0
x < -1 or x > 1
Thus the domain has no boundary to consider.
A critical point is where the derivative is 0:
1 + 2x/(x²-1) = 0
x² + 2x - 1 = 0 (1)
x = (-2 ± √(4 + 4))/2 = -1±√2
The solution -1+√2 is in the interval (0,1), where f(x) is undefined.
So we have just one critical point, let's call it c = -1-√2.
To see whether it is local minimum or maximum, see whether f"(c) > 0 or f"(c) < 0.
To make the calculation easier, notice that the point c satisfies (1), so
c² - 1 = -2c
So
f"(c) = 2/-2c - 4c²/4c² = -1/c - 1 = -1/(-1-√2) - 1 = -√2/(1+√2) < 0
Therefore the critical point c is a local maximum.
But it is only LOCAL, not GLOBAL.
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.


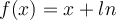




Mark M.
Why should you get credit if a tutor does the work?05/19/21