Daniel B. answered • 05/13/21
A retired computer professional to teach math, physics
Any maximum/minimum value of function on a closed set is either
a critical point, or lies on the boundary.
To find maximum/minimum on the boundary we use the method of Lagrange
multipliers, which I assume is meant by "level curves and gradients".
1)
f(x,y) = x + y + 1
To find critical points:
∂f/∂x = 1
∂f/∂y = 1
Therefore there no critical points.
To find maximum/minimum along
x²+y²=1 (1)
we form
F(x,y,λ) = x + y + 1 - λ(x² + y² - 1)
∂F/∂x = 1 - 2λx = 0 ==> x = 1/2λ
∂F/∂y = 1 - 2λy = 0 ==> y = 1/2λ
Plugging it into the constraint (1)
1/4λ² + 1/4λ² = 1
λ = ±1/√2
This gives two points (x, y)
(√2/2, √2/2) and (-√2/2, -√2/2).
The first is global maximum and the second is global minimum.
2)
f(x,y) = x² + 2y²
To find critical points:
∂f/∂x = 2x
∂f/∂y = 4y
So we have one critical point (0,0).
In order to see if it is a local minimum, maximum, or saddle point,
we need the Hessian matrix H:
H = | 2 0 |
| 0 4 |
We see that its eigenvalues are positive (and so is the determinant).
Therefore the point (0,0) is a local minimum.
To compute the maximum/minimum along the boundary we again form
F(x,y,λ) = x² + 2y² - λ(x² + y² - 1)
∂F/∂x = 2x - 2λx = 0 ==> x(1 - λ) = 0
∂F/∂y = 4y - 2λy = 0 ==> y(2 - λ) = 0
The above two equations are satisfied if
- x = 0, in which case (1) implies y = ±1, which gives points (0, 1), (0, -1)
- y = 0, in which case (1) implies x = ±1, which gives points (1, 0), (1, 0)
- λ = 1, in which case y = 0 -- already covered above
- λ = 2, in which case x = 0 -- already covered above
So in total we have the following candidates and their corresponding values of f
f(0,0) = 0,
f(0,1) = 2,
f(0,-1) = 2,
f(1,0) = 1,
f(-1,0) = 1.
Therefore (0,0) is global minimum and both (0,1),(0,-1) are global maxima.
3)
f(x,y) = x² - 2y²
∂f/∂x = 2x
∂f/∂y = -4y
So we have one critical point (0,0).
In order to see if it is a local minimum, maximum, or saddle point,
we need the Hessian matrix H:
H = | 2 0 |
| 0 -4 |
Its determinant
D = ∂²f/∂x² ∂²f/∂y² - ∂²f/∂x∂y ∂²f/∂y∂x = -8 < 0
Therefore (0,0) is a saddle point.
To compute the maximum/minimum along he boundary we again form
F(x,y,λ) = x² - 2y² - λ(x² + y² - 1)
∂F/∂x = 2x - 2λx = 0 ==> x(1 - λ) = 0
∂F/∂y = -4y - 2λy = 0 ==> y(2 + λ) = 0
The above two equations are satisfied if
- x = 0, in which case (1) implies y = ±1, which gives points (0, 1), (0, -1)
- y = 0, in which case (1) implies x = ±1, which gives points (1, 0), (1, 0)
- λ = 1, in which case y = 0 -- already covered above
- λ = -2, in which case x = 0 -- already covered above
So in total we have the following candidates and their corresponding values of f
f(0,1) = -2,
f(0,-1) = -2,
f(1,0) = 1,
f(-1,0) = 1.
Therefore (0,1),(0,-1) are global minima and (1,0),(-1,0) are global maxima.


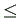 =1
=1


