Length of Planar Curves

Question

What is the length of the curve 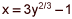 from y = 0 to y = 8? (4 points)

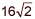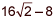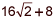	None of these

Answer 1

For an easier integration, develop (from x = 3y^(2/3) − 1): (x + 1)/3 = y^(2/3) which goes to

[(x + 1)/3]^1.5 = {y^(2/3)}^1.5 or y = [(x + 1)/3]^1.5. Then dy/dx equals (1.5/3)[(x + 1)/3]^0.5 or

0.5[(x + 1)/3]^0.5. Now take (dy/dx)² as 0.25[(x + 1)/3].

From L = ∫√{1 + (dy/dx)²}dx, construct L = ∫√{1 + (x + 1)/12}dx or L = ∫{(x + 13)/12}^0.5dx.

∫{(x + 13)/12}^0.5dx integrates to (2/3×12){(x + 13)/12}^1.5 or 8{(x + 13)/12}^1.5.

From y^(2/3) = (x + 1)/3 , determine 8^(2/3) = (x + 1)/3 which gives x = 11.

From y^(2/3) = (x + 1)/3 , determine 0^(2/3) = (x + 1)/3 which gives x = -1.

Final evaluation of [8{(x + 13)/12}^1.5|_{(from -1 to 11)}] goes to [(8×2^1.5) − (8×1^1.5)] or 16√2 − 8√1

or 16√2 − 8 (equal to 14.627417 units of length).