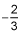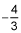Which of the following is the coefficient of x3 in the Maclaurin series for f(x) = sin(2x)?

Question

Which of the following is the coefficient of x³ in the Maclaurin series for f(x) = sin(2x)?

Answer 1

Recall that the Maclaurin expansion for a function is the Taylor series centered on x₀ = 0.

So, in general, f(x) ~ ∑_n=0^∞ f⁽ⁿ⁾(0)·xⁿ/n! where f⁽ⁿ⁾(x) is the n^th derivative.

So the cubic coefficient would be f^"'(0) / 3!.

f(x) = sin2x

f^'(x) = 2cos2x

f^"(x) = -4sin2x

f^"'(x) = -8cos2x

f^"'(0) = -8 and the coefficient of x³ in the expansion is - 4/3.

Answer 2

sinx = x - x³/3! + x⁵/5! - ...

by replacing x by 2x we get sin2x = 2x - 8x³/3! + 32x⁵/5! - ...

So coefficient of x³ is - 8/3! = - 4/3

Answer: - 4/3