Yes. This series is divergent. In fact, convergence or divergence does NOT depend on the terms at the beginning of the series, it depends instead on the series' "eventual" behavior. This is why so many of the convergence tests depend on examining the limit as n approaches infinity of the nth term (or the nth root of the nth term or the ratio of the n + 1st term to the nth, etc.). Put simply, you could eliminate any finite number of terms from a divergent series (at the beginning, as in the sequence above, or anywhere) and the series would still diverge.
Franco C.
asked • 03/27/21Series tests Harmonic
Does the harmonic series apply to series in which n doesn't start at 1 or zero?
For example would it apply for the series?
More
1 Expert Answer
Still looking for help? Get the right answer, fast.
Ask a question for free
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Find an Online Tutor Now
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.


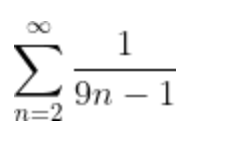




Franco C.
Thank You!03/28/21