The lower estimate will be the left-hand sum (since x2 increasing on [0,4]). The upper will be the right-hand sum. Left and right-hand sums have to do with at which x-values we evaluate the function in order to get the heights of the rectangles so we can sum their areas. The interval is [0,4] so 4 rectangles (and trapezoids) will mean 4 subintervals of = width at [0,1] , [1,2] , [2,3], and [3,4].
The left-hand sum uses the y-values associated with the left endpoints of those subintervals, namely 0, 1, 2, and 3. f(0) = 0 , f(1) = 1, f(2) = 4, and f(3) = 9. So the lower sum is 1·(0 + 1 + 4 + 9) = 14.
The righthand sum uses the righthand endpoints, 1, 2, 3, and 4. f(4) = 16, so upper sum is 1·(1 + 4 + 9 + 16) = 30.
Lastly, the trapezoidal sum can be obtained with this formula Strap = (b-a)/(2n)·(f(a) + 2f(x1) + ... + 2f(xn-1) + f(b)). So Strap = 1/2(0 + 2 + 8 + 18 + 16) = 22.
It is a fairly trivial proof to show that the trapezoidal sum is always the average of the left- and right-hand sums.

Josh F.
03/25/21


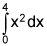




Ssierra K.
Thank you this helped very much!03/25/21