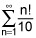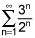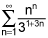Which of the following series is/are convergent?

Question

Which of the following series is/are convergent?

1. 
2. 
3. 

A	I and II
B	II and III
C	All of them
D	None of them

Answer 1

1) This first one, since it is an infinite series involving factorials, we can just use the ratio test to see if this one converges.

Let's take two arbitrary terms, term n, and term n+1. If we take the ratio of these two terms, what we get is:

((n+1)!/10)/(n!/10) = (n+1)!/n! = n+1 > 1.

Since the ratio of these two terms is greater than 1, the series does not converge.

2). Another way of writing this series is Σ_{n = 1}^∞ (3/2)ⁿ. This is just a geometric series, with a ratio of 3/2 > 1. Since the ratio of this geometric series is greater than 1, it does not converge.

3) This one will be a bit hand-wavy. It is clear in the long run that the numerator is growing much faster than the denominator, so in the long run, there is no way the limit of each term is tending to zero as n grows large, which means the series doesn't converge.

Since none of the series converge, the answer is d.