Tom K. answered • 03/12/21
Knowledgeable and Friendly Math and Statistics Tutor
As f'(x) < 0 throughout the interval, the max of these values will be the left endpoint, and the min will be the left endpoint. As f'' < 0, the curve and midpoint is above the trapezoid. Then, consider the trapezoid formed using the midpoint with the slope equaling the slope at the midpoint; the area of this is the same as the area with the midpoint rule. As f'' < 0, the actual curve will be below the trapezoid, so the area will be less. Thus, we now have our order.
From max to min, it is left, midpoint, actual, trapezoid, right.
Thus, the answer is left .8895; midpoint .8421; actual .8410; trapezoid .8405; right .7915
Reordering to match the problem, we have
right .7915
left .8895
midpoint .8421
actual .8410
trapezoid (1 + .3)/2 = .65
The order
trapezoid .8405
As an example to show the order is reasonable, consider f(x) = 1 - .7x^2 and one interval; we have the right curvature and proper values of f(0) and f(1), with f' < 0 for x > 0.
right .3
left 1
midpoint 1 - .7(.5)^2 = .825
actual using I[a,b] for the integral from a to b and E[a, b] the evaluation from a to b
I[0,1] 1 - .7x^2 dx = x - 7/30x^3 E[0, 1] = 23/30 = .76667
trapezoid (1 + .3)/2 = .65
Order from larges to smallest is left, midpoint, actual, trapezoid, and right, just as we said.


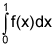 . The estimates were 0.7915, 0.8405, 0.8410, 0.8421 and 0.8895, and the same number of subintervals were used in each case. Match the rule to its estimate.
. The estimates were 0.7915, 0.8405, 0.8410, 0.8421 and 0.8895, and the same number of subintervals were used in each case. Match the rule to its estimate.

