
Doug C. answered • 12/25/25
Math Tutor with Reputation to make difficult concepts understandable
For a curve defined parametrically in terms of t, dy/dx = (dy/dt) / (dx/dt). The curve will have horizontal tangent lines when dy/dt = 0, provided dx/dt ≠ 0.
dy/dt = 6t2 +18t - 24
dx/dt = 3t2 +12t + 9
So, dy/dx = [(6t2 + 18t -24) / (3t2 + 12t + 9)]
dy/dx = 0 when the numerator of that fraction equals zero:
6t2 + 18t - 24 = 0
t2 + 3t - 4 = 0
(t + 4)(t - 1) = 0
t = -4 or t = 1.
dx/dt does not equal zero at those values of t, so the graph has horizontal tangent lines at the points where t = -4 or t = 1.
If you wanted to know where the graph has vertical tangent lines (if any), that will be where the denominator (dx/dt) is equal to zero (and dy/dt ≠ 0).
desmos.com/calculator/q8msqih5sa
Use the slider on "v" to see the graph being traced out.


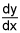 = 0 for the parametric equations x = t
= 0 for the parametric equations x = t

