
Neha S.
asked • 03/02/21Is the answer 4?
What is the length of the curve with parametric equations x = t - cos(t), y = 1 - sin(t) from t = 0 to
t = π? (20 points)
| 8 | |
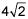 |
|
| 4 | |
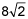 |
1 Expert Answer
Here, dx/dt is 1 + sin t; (dx/dt)2 is 1 + 2sin t + sin2t.
Then take dy/dt as -cos t and (dy/dt)2 as cos2t.
Next construct curve length or s equal to ∫(from 0 to π)√[(dx/dt)2 + (dy/dt)2]dt.
Place results above and put down s = ∫(from 0 to π)√[1 + 2sin t + sin2t + cos2t]dt.
Rewrite this last integral as s = ∫(from 0 to π)√[2 + 2sin t]dt or √2∫(from 0 to π)√[1 + sin t]dt.
Using sin2θ + cos2θ = 1 and sin 2θ = 2sin θcos θ, develop s = √2∫(from 0 to π)√[1 + sin 2(t/2)]dt.
Express s again as √2∫(from 0 to π)√[sin2(t/2)+ 2sin (t/2)cos (t/2) + cos2(t/2)]dt or
√2∫(from 0 to π)√{ [sin (t/2)+ cos (t/2)]2 }dt which reduces to √2∫(from 0 to π){ cos (t/2)+ sin (t/2) }dt.
Integrate this last to √2[2sin (t/2) − 2cos (t/2) | (from 0 to π)].
Apply limits of integration to gain [2√2sin (π/2) − 2√2cos (π/2) − 2√2sin (0/2) + 2√2cos (0/2)]
which calculates to 2√2[1 − 0 − 0 + 1] or 4√2 units of length.
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.






Mark M.
Is this from a test/quiz/exam? Getting and giving assistance of such is unethical.03/03/21