
Yefim S. answered • 03/02/21
Tutor
5
(20)
Math Tutor with Experience
y' = secxtanx; y = ∫secxtanxdx = secx + C;
y(0) = sec0 + C = 1; C = 0
So, y = secx
Nic C.
asked • 03/02/21Find the equation of the curve that passes through the point (x, y) = (0, 1) and has an arc length on the interval 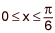 given by the integral
given by the integral 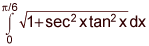
| y = tan(x) | |
| y = tan-1(x) | |
| y = sec(x)tan(x) | |
| y = sec(x) |

Yefim S. answered • 03/02/21
Math Tutor with Experience
y' = secxtanx; y = ∫secxtanxdx = secx + C;
y(0) = sec0 + C = 1; C = 0
So, y = secx
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.