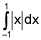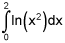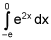urgent calculus question

Question

 

Which of the following is an improper integral?

	None of these

Answer 1

In order to identify an improper integral is to consider the domain of the integrand and compare it with the limits of integration.

In your case, the first option is the absolute value of whose domain is R (real numbers) and you see that the limits of integrations are -1 and 1, so there are no infinities of the function |x| between -1 and 1.

The third integrand is the exponential function whose domain is again R (all real numbers) and there are no infinities within the limits of integrations (-e and 0)

The second integrand is a log(x²) which has a singularity at x=0, and you can see that x=0 is the lower limit of integration. Hence, the integrand is not defined at x=0 which implies that the integral is an indefinite integral.

So the answer is the second.

Best,

Davide