calculus question

Question

 What is the best method to evaluate  ?

	Integration by parts
	Rewrite the integral using long division
	Rewrite the integral using partial fractions
	Use a substitution

Answer 1

Integration by parts is not a viable option since all terms are algebraic and no other special algebra is involved (trigonometry, exponentials, and the like).

Rewriting the integral using long division is a viable option since it will "simplify" the problem, but you'll use another method to fully solve the integral in a later part of long division.

Rewriting the integral using partial fractions would work if there were a denominator with multiplication of algebraic terms, not just one.

This leaves using a substitution to be the best option to evaluate the integral.

To solve it:

u = x + 1 u + 1 = x + 2 u + 2 = x + 3

du = dx

∫ [ ( u + 1 ) ( u + 2 ) / u ] du = ∫ [ ( u² + 3 u + 2 ) / u ] du = ∫ ( u + 3 + 2 / u ) du

∫ ( u + 3 + 2 / u ) du = u² / 2 + 3 u + 2 ln| u |

∫ [ ( x + 2 ) ( x + 3 ) / x ] dx = ( x + 1 )² / 2 + 3 ( x + 1 ) + 2 ln| x + 1 |

I hope this helps! Message me in the comments if you have any questions or if I did anything wrong!

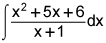Answer 2

Rewrite the integrand using long division: (x² + 5x + 6) / (x + 1) = x + 4 + 2 / (x + 1)

(The integral then becomes 1/2x² + 4x + 2ln|x + 1| + C.)

Answer 3

We have to use long division: (x² + 5x + 6)/(x + 1) = x + 4 + 2/(x + 1).

So, ∫(x² + 5x + 6)/(x + 1)dx = ∫(x + 4 + 2/(x + 1))dx = x²/2 + 4x + 2lnIx + 1I + C