Calculate dy/dx

Question

y=x -3/ x+3

dy/dx=__?

Answer 1

It's a little unclear from the way you've written it, but I'll assume the (x-3) is all under the sq. root, as is (x+3).

If that's the case, it will be easier to write the function as y = √((x-3)/(x+3)), that way we only have to deal with the square root once. We will need to use both quotient rule and chain rule, since the function under the sq. rt. is a quotient.

dy/dx = [((x+3) - (x-3)) / (x+3)²][1 / 2√((x-3)/(x+3))] = [ 6 / (x+3)²] [1 / 2√((x-3)/(x+3))] = 3 / [(x+3)²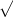√((x-3)/(x+3))]