Kim G. answered • 01/21/21
Yale student pursuing MA in statistics and PhD in public health
Hi Eddy - great questions! It looks like this question is asking us to understand the logic behind limits for multiple functions, even if we don't necessarily have exact equations for them. Here's how I'd approach it.
a) To find the limit as x -> 2 of f(x) + g(x), it helps to remember an important property of limits: that the limit of the sum of two functions equals the sum of the limits. So that means we separately have to find the limit as x -> 2 of f(x) and the limit as x->2 0f g(x), and then add them together. Let's do that:
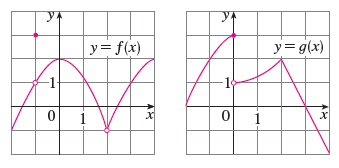
i) f(x): Let's look at x = 2 on the graph of f. Starting from x = 1 and moving towards x = 2 (the "left-hand" side), we see that as we get closer and closer to x = 2, the function f(x) gets closer and closer to f(x) = -1 (the point (2,-1)). So we have a good guess that the limit = 2. Importantly, we have to check that the "right-hand" limit equals the same thing. Starting from x = 3 and heading towards x = 2, we see the function heading towards the same point (2,-1) (i.e. f(x) = -1). Therefore, our limit for f(x) is -1.
ii) g(x): Let's look now at the graph of g(x). Using the same logic, I can start at x = 1 and move towards x = 2. As I do that, I notice the graph gets closer to the point (2, 2) (i.e. g(x) = 2). The same checks out if I start from x = 3 and move the other way, so our limit for g(x) is 2.
Add those together and we have our answer: -1 + 2 = 1.
Now that we've established the basic logic of finding a limit in Part (a), we can approach the others in a similar way:
b) Again here, I can use a similar property to the one used above: that the limit of the difference equals the difference of the limits. That means that all I have to do is find the limit as x -> 0 of f(x), find the limit as x -> 0 of g(x), and then subtract the two. But wait! I immediately see a problem. The graph of g(x) has two "limits" at x = 0; when you start from -1 and head towards zero, we approach the point (0,3), but if we start from 1, we approach (0,1). Since the right hand and left hand limit don't equal each other, the limit does not exist for g! That means that the limit doesn't exist for the whole thing here (at least, as x -> 0).
c) Similar to parts (a) and (b), the limit of the product equals the product of the limit. So let's again look at f(x) and g(x) separately. I'm going to go out of order for this one, and you'll see why. The limit for g(x) is pretty straightforward: we start at x = -2 and head towards x = -1 to find the graph approaching (-1, 2). Same thing for the other side - so the limit as x -> -1 of g(x) is 2.
Now, what's going on with f? It looks like, if we look left of the y axis, we have a smooth curve at every point except x = -1, where there's a "gap" at (-1,1) and a "jump" to the point (-1,3). Does that mean that our answer is 3, since that's what f(x) equals when we plug in x = -1? Not quite! This is where limits are different from our usual algebra. We use the same logic as we've used for Parts (a) and (b) - start at -2 and head towards -1. What does the function approach? Looks like the point (-1,1). Same thing if we start from x = 0. So the limit as x -> -1 of f(x) is actually 1! Multiply that with the limit for g(x) and we get 2 x 1 = 1.
d) Again noting that the limit of the product equals the product of the limits, this one is a lot more straightforward than parts (b) and (c) - since there are no weird gaps, jumps, or sharp points for either of the graphs at x = 3, we can just multiply f(3) and g(3) together to get our answer - and since g(3) equals zero, and anything times zero equals zero, our limit will be zero.
e) I'm having a bit of trouble understanding exactly what this question is asking (simply because Wyzant sometimes makes it difficult to use mathematical notation), but here's my best shot. Here we use the principle that we can "pull out" constant coefficients, and we simply have to plug in x=2 to evaluate the x part. Here's what I mean: In part (a), we found that the limit as x->2 of f(x) = -1. Multiply that by 2x to get -2x. Now, plug in x = 2 (since that's the x value that this question asks about in the first place!) and we find our limit to be -2 x 2 = -4.
f) Finally, this question asks us to look again at something we discovered in Part (c) - that f(-1) isn't necessarily equal to the limit as x -> -1 of f(x). Again, if we look left of the y-axis, we see that f(x) is a smooth curve at every point except x = -1, where there's a "gap" at (-1, 1) and a "jump" to (-1,3). Note that the point (-1,3) is the one that's actually filled in: this means that f(-1) = 3. Now, we already know from part (c) that the limit as x -> -1 of g(x) is 2: so our final answer is 3 + 2 = 5.
Hope this helps! LMK if you have any other questions :)