Alex R.

asked • 12/13/20

Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle. Finally, find the area of the region.

y=x2−3x, y=5x

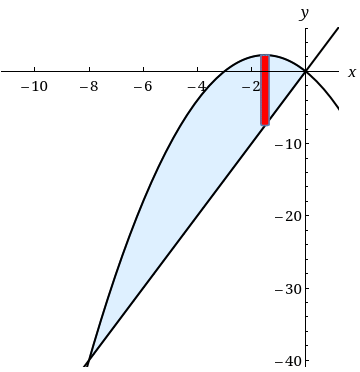
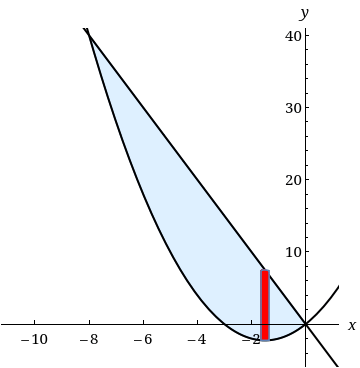
WebAssign Plot

 

WebAssign Plot

 

WebAssign Plot

 

WebAssign Plot





David M.

To determine whether or not to integrate with respect to x or y, You have to consider all possible representative rectangles with a vertical or horizontal length and minimal width filling up the area of consideration. The length must either be the difference between the y values of two curves no matter where the rectangles are formed or the difference between the x values of the two curves no matter where the rectangles are formed. If vertical lengths do not work then try horizontal lengths. If both fail, consider subdividing the problem into sections of the area to be determined and adding up your result. If you end up with vertical rectangles, your width will be a horizontal dx. If you end up with horizontal rectangles, your width will be a vertical dy. A dx width means you will be integrating with respect to x between two x values; and a dy width means you will be integrating with respect to y between two y values as the interval of integration. In the first example you have given, if you had tried horizontal rectangles, the rectangles in the portion above the x axis would the length would be the difference in x values of the same curve instead of the difference in x values between the two curves, so a horizontal rectangle would not work, so dy would not work for the width and integrating with respect to y would not work.
Report

12/18/20

1 Expert Answer

By:

Still looking for help? Get the right answer, fast.

Ask a question for free

Get a free answer to a quick problem.
Most questions answered within 4 hours.

OR

Find an Online Tutor Now

Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.