
Al P. answered • 12/05/20
Online Mathematics tutor
The definite integral evaluates to y = 6x / (x+1)
dy/dx = ((x+1)(6) - 6x(1) ) / (x+1)2 = 6 / (x+1)2
d2y / dx2 = -6(2)(x+1) / (x+1)4 = -12 / (x+1)3
The interval on which y is concave up corresponds to the interval on which d2y / dx2 > 0. Due to the -12 in the numerator, this happens wherever (x+1)3 < 0:
(x+1)3 < 0 on the interval x ∈ (-∞, -1)


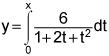 is concave up
is concave up

