Find the arc length of the curve from t = 0 to t = 2

Question

Find the arc length of the curve from t = 0 to t = 2 whose derivatives in parametric form are 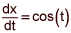 and  .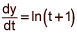

Type your answer in the space below and give 2 decimal places. If your answer is less than 1, place a leading "0" before the decimal point (ex: 0.48)

I got 1.91.

Answer 1

I Acr Length is found as

L=∫₀² √((dx/dt)²+(dy/dt)²) dt =|just plug in instead dx/dt and dy/dt and evaluate the integral|

= ∫₀² √(cos²t+ln²(t+1)) dt = 1,91...