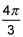CHECK MY ANSWER CALCULUS POLAR CURVES NEED HELP ASAP PLS!

Question

Find the values of θ at which there are horizontal tangent lines on the graph of r = 1 + sin θ. (4 points)

ANSWER CHOICES

I CHOSE THIS	,  ,  ,
	,  ,
	,  ,  ,
	,  ,

Answer 1

If you plot the polar curve, you get an upside down cardoid. Looks line horizontal tangents touch the curve in only three places, at θ = π/2, 7π/6 and 11π/6.

So horizontal lines are at points when dy/dx = 0.

dy/dx = (dr/dθsin(θ) + rcos(θ))/(dr/dθcos(θ)-rsin(θ))

r = 1+sin(θ), dr/dθ = cos(θ)

So:

cos(θ)sin(θ) + (1+sin(θ))cos(θ) = 0 -> cos(θ)(2sin(θ)+1) = 0

cos(θ) = 0 at θ= π/2

sin(θ) = -1/2 at θ=7π/6 and 11π/6

This is the second selection.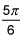
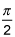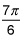
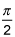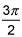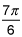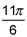
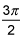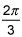