A ladder 10 ft long rests against a vertical wall.

Question

If the bottom of the ladder slides away from the wall at a rate of 1.4 ft/s, how fast is the angle between the ladder and the ground changing when the bottom of the ladder is 6 ft from the wall? (That is, find the angle's rate of change when the bottom of the ladder is 6 ft from the wall.)

Answer 1

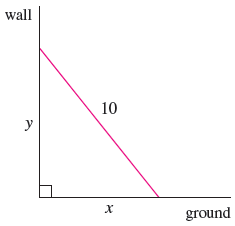
We're asked to dθ/dt, or θ', so first we need to find an equation that relates the angle between the ladder and ground, θ, and the distance x. From trigonometry, we know that

cosθ = adjacent/hypoteneuse

= x/10 .

Now, remember that both θ and x are functions of t, meaning they change as time changes. We need that info because our next step is to differentiate, and we'll need to use the chain rule to do so.

d/dt(cosθ) = d/dt(x/10)

-sinθ*θ' = (1/10) x' .

θ' and x' are both the results of the chain rule.

Now, fortunately we can fill in the missing information. We were given that the bottom of the ladder is moving at 1.4 ft/s, so

x' = 1.4.

We also know that this moment is when the bottom of the ladder is 6 feet from the ground, or

x=6.

Using the Pythagorean Theorem, we can solve for y :

6² + y² = 10²

y² = 64

y = 8.

This is important because we have a sinθ in our new derived equation, but because we know the values of x, y, and the hypotenuse,

sinθ = opposite/hypotenuse

= y/10

=8/10.

We can plug this back in to our equation and we get:

-(8/10)θ' = (1/10)(1.4)

θ'= -(10/8)(1/10)(1.4)

θ' = -11.2 deg/sec

Hope this helps!