Tom K. answered • 10/21/20
Knowledgeable and Friendly Math and Statistics Tutor
Draw a circle centered at the origin. While you can solve using implicit differentiation that dy/dx = -x/y, note that you can easily reason out the sign. In the first and third quadrants, the slope of the tangent is negative (obvious from the picture),and x/y is positive. In the second and fourth quadrants, the slope of the tangent is positive and x/y is negative. Thus, we don't have a circle, so we are left with the two hyperbolas. Plug in x and y and you get that the solution is x^2 - y^2 = -5
Now, the fancier way using implicit differentiation.
x^2 + y^2 = c (either 13 or 25)
2xdx + 2ydy = 0
2ydy = -2xdx
dy/dx = -2x/2y = -x/y
For the hyperbolas,
x^2 - y^2 = c
2xdx - 2ydy = 0
2ydy = 2xdx
dy/dx = 2x/2y = x/y


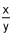 . Find the equation of the curve if the point (2, -3) is on the curve. (5 points)
. Find the equation of the curve if the point (2, -3) is on the curve. (5 points)

