
Yefim S. answered • 09/22/20
Math Tutor with Experience
f(x) = 1/ (√2 - 0) ∫0√2(2 - x2)dx = 1/√2(2x - x3/3)0√2= 1/√2(2√2 - 2√2/3) = 4/3.
So 2 - x2 = 4/3. x2 = 2/3 and x = ±√2/3. Inside our interval we have x = √2/3.
Last answer is right, x = √2/3
Lilah B.
asked • 09/22/20
Determine if the Mean Value Theorem for Integrals applies to the function f(x) = 2 - x2 on the interval 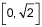 . If so, find the x-coordinates of the point(s) guaranteed by the theorem. (5 points)
. If so, find the x-coordinates of the point(s) guaranteed by the theorem. (5 points)
Answer Choices:
| No, the Mean Value Theorem for Integrals does not apply | |
Yes, 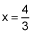 |
|
Yes, 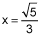 |
|
Yes, 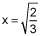 |

Yefim S. answered • 09/22/20
Math Tutor with Experience
f(x) = 1/ (√2 - 0) ∫0√2(2 - x2)dx = 1/√2(2x - x3/3)0√2= 1/√2(2√2 - 2√2/3) = 4/3.
So 2 - x2 = 4/3. x2 = 2/3 and x = ±√2/3. Inside our interval we have x = √2/3.
Last answer is right, x = √2/3

Jason A. answered • 09/22/20
BS Chemical Engineering
Hi there Lilah!
The Mean Value Theorem for Integrals states that a continuous function on a closed, bounded interval has at least one point where it is equal to its average value on the interval.
This means that for a given area under the curve of your function, there's a point on the curve, c, where you can draw a box that has the same area. The box and the curve intersect at Point c.
I'm assuming you don't need to prove that the function is continuous so that we can skip to taking integrals:
f(x) = 2 - x²
a = 0
b = √2
A = ⌠a 2 - x² dx
⌡b
= 2x - 1/3 * x³ | b
| a
= [ 2 √2 - 1/3 * (√2)³ ] - [ 2*0 - 1/3 * 0³ ]
A = 2√2 - 2√2 / 3
= 6√2 - 2√2
3
= 4√2
3
So now we have the area under the curve from 0 to √2, now let's find the height of the box since we already know the length (0 to √2).
A = l*w
l = b - a = √2 - 0 = √2
w = A / l
= 4√2 * 1
3 √2
= 4/3
Now we have the height of the box. Finally, we want to know if there's a point x within the bounds that can gives us this value in the original function. So we solve for x and find possible values:
f(x) = 2 - x²
f(x) - 2 = -x²
2 - f(x) = x²
√ ( 2 - f(x) ) = x
Now we plug in numbers:
x = √ (2 - 4/3)
= √ (2/3) = 0.816
This is in fact between the bounds of 0 and √2 (which is 1.414), so our answer satisfies the mean value theorem for integrals along these bounds. Be sure to check that last detail in case a test problem tries to trick you there!
Hope this helps! Please reach out with any further questions!
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.