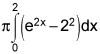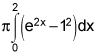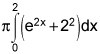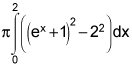Calculus Please help!

Question

Which of the following integrals will find the volume of the solid that is formed when the region bounded by the graphs of y = e^x, x = 2, and y = 1 is revolved around the line y = -1. (5 points)

Answer Choices:

Answer 1

V = π ∫ [f(x)² - g(x)²] dx

where f(x) is the top curve, g(x) is the bottom curve, and dx is the width

distance from the top curve to the axis of rotation = e^x - (-1) = e^x +1

distance from the bottom curve to the axis of rotation = 1 - (-1) = 2

The left bound is the x-value where y = e^x crosses y = 1, which is at x = 0. The right bound is the x-value where y = e^x and y = 1 cross x = 2, which is at x = 2. The integral will be taken from x = 0 to x = 2.

V = π ∫ [(e^x +1)² - (2)²] dx

You answer is D

Answer 2

Last integral is right to give this volume