For the function f whose graph is given, state the value of each quantity, if it exists. (If an answer does not exist, enter DNE.)

Question

For the function f whose graph is given, state the value of each quantity, if it exists. (If an answer does not exist, enter DNE.)

(a)    lim x→1 f(x)

(b)    lim x→3⁻ f(x)

(c)    lim x→3⁺ f(x)

(d)    lim x→3 f(x)

(e)    f(3)

Answer 1

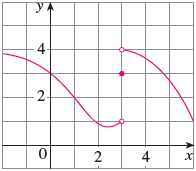
a) When evaluating limits, it is important to first check whether a limit exists. The easiest way to do this is to take your pencil and follow the function from the right of x = 1 (The 1+ limit) and the left of x = 1 (The 1- limit) to where x = 1 and see if you get to the same y point. Here we get y = 2 for both, so the the answer is 2.

b) Here we are being asked to take the left sided limit (3-) so we take our pencil somewhere around x = 0, y = 3 on the function and trace it towards x = 3. Here we see that as we get closer and closer to x = 3, the y will get closer to 1 (the bottom open circle), so the answer is 1

c) Very similar to part b, we now take the right sided limit (3+) so we start our pencil around x = 6, y = 1 on the function and trace it towards x = 3. Here we see that as we get closer and closer to x = 3, the y will get closer to 4 (the top open circle), so the answer is 4

d) Here they are asking for the total limit as x approaches 3. In order for a limit to exist, it needs to approach the same value for both the left and right sided limits. Luckily, we've already done these steps before in parts b and c. Since in part b (left sided) we got 1 and in part c (right sided) we got 4, the left and right sided limits are different and thus the total limit does not exist. Answer is DNE

e) Here we are not taking a limit but asked just to evaluate the function at x = 3. This is different than a limit because for a limit you never actually get to the point you're taking the limit of (x = 3 from the left or right), but when asking the value of a function you're actually at the point x = 3. This is where the open and closed circles come into play. An open circle, just like on a number line, means NOT including this point. The closed circle however, does mean including this point. Another way to think of it is that if there is an open circle and closed circle on the same x (in this case x = 1), the open circle is where a limit will approach to, but the closed circle is where the function will actually go when evaluated. I also like to think of the open circle as a portal that jumps to the closed circle when asked what the actual value of a function is at that specific x point. In this case the closed circle for x = 3 is at y = 3, so the answer is 3.