Let S be the solid obtained by rotating the region shown in the figure about the y-axis. (Assume a = 6 and b = 3.)

Question

Find its circumference c and height h

c(x)=______

h(x)=_______

Use shells to find the volume V of S

V=_______

Answer 1

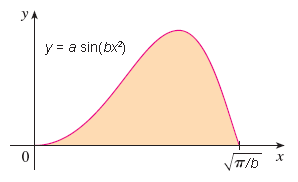
To find the volume of the solid that results from rotating the function about the y-axis, we will create many 3D shells, find the volume of each one, and add them all together. Actually, the process boils down to expressing a general 3D shell as a function, and then integrating the function over the interval of x seen in the graph.

Each shell's volume can be found by multiplying (1) its circumference, (2) its height, and (3) its width.

The circumference of each shell is

C = 2πr where the radius is equal to x.

Thus,

C = 2πx

The height of each shell is equal to f(x), which is given.

h(x) = f(x) = 6sin(3x²)

Finally, the width of each shell is simply

width = dx

(Each shell is made up of a rectangle of width = dx and height = f(x) that is rotated about the y-axis at a circumference, 2πx.)

To find the volume, all we have to do is multiply the three parameters (height, width, and circumference) and integrate over the interval x = [ 0, √(π/3) ].

V = ∫ (2πx)*f(x) (dx) evaluated over the interval [ 0, √(π/3) ]

V = 2π ∫ (x) (6)sin(3x²) ( (dx)

V = 2π ∫ (6x) sin(3x²) (dx)

V = 2π * [ -cos(3x²) ] ₀^√(π/3)

V = 2π * [ -cos(3(π/3)) - (-cos(0)) ]

V = 2π * [ -cos(π) + cos(0) ]

V = 2π * (1 + 1)

V = 4π

Answer 2

desmos.com/calculator/lm7vnvll9q