law of cosines help

Question

Use the Law of Cosines to determine the indicated angle θ. (Assume a = 61.01, b = 36.67, and c = 42.95. Round your answer to two decimal places.)

θ =   °

Answer 1

[ALL STEPS EXPLAINED]

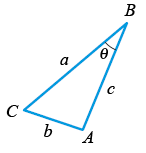
We use the Law of Cosines, which says:

a² = b² + c² - 2bc Cos(A)

b² = a² + c² - 2ac Cos(B)

c² = a² + b² - 2ab Cos(C)

STEP 1 - Solve for angle B:

b² - a² + c² = -2ac Cos(B)

(b² - a² + c² ) / -2ac = Cos(B)

arccos((b² - a² + c² ) / -2ac) = arccos (Cos(B))

arccos((b² - a² + c² ) / -2ac) = B

B = arccos((b² - a² - c² ) / -2ac)

STEP 2 - Calculate the values:

(Typically, 2 decimal places is ok)

a² = 61.01² = 3722.22

b² = 36.67² = 1344.69

^c2 = 42.95² = 1843.41

2ac = 2*61.01*42.95 = 5240.76

STEP 3 - Plug in values

B = arccos((1344.69 - 3722.22 - 1843.41 ) / -5240.76)

B = arccos(-4220.94 / -5240.76)

B = arccos(0.8054)

ANSWER:

B = 0.69 radians

B = 36.35 degrees

____________________________________________________________________________________

*Note: Using more significant digits, the answer becomes B=36.32662, (or 36.33 degrees)

(RELATED CONCEPTS)

Note 1: Convert degrees to radians: 36.33 degrees * (3.14 radians / 180 degrees) = 0.63 radians

Note 2: Change calculator mode to RAD or DEG to get the correct value for arccos and cos^-1

Note 3: arccos(x) = cos^-1(x) -- the same

Note 4: cos^-1(x) is different than cos(x)^-1 = 1/cos(x) = sec(x), do not get them mixed up

Answer 2

c^2=a^2+b^2-2ab*cos(c)

42.95^2=61.01^2+36.67^2-2(61.01)(36.67)cos(c)

1844.7025=3722.2201+1344.6889-4474.4734cos(c)

1844.7025=5066.909-4474.4734cos(c)

-3222.2065=-4474.4732cos(c)

cos(c)=3222.2065/4474.4732

cos(c)=0.7201

c=cos^-1(0.7201)

c=43.9347 degrees

Repeat to solve for angles a and b using the below formulas

a^2=b^2+c^2-2bc*cos(a)

b^2=a^2+c^2-2ac*cos(b)

Angle a = 99.74 degrees

angle b = 36.33 degrees

angle c = 43.93 degrees