This can be solved with simple substitution.
8
We know that ∫ f(x) dx = 18
0
We can rewrite the integral we wish to evaluate by defining a variable u = 2x. Now we can find du/dx = 2. This is useful because now we have set up a differential equation where we can write dx = (1/2) du.
4 8
Now we can substitute our values in: ∫ f(2x) dx = ∫ (1/2) * f(u) du
0 0
Notice we changes our bounds since we are no longer integrating with respect to x. Simply plug in the x-value bounds into our equation for u which was u = 2x, hence we are now integrating from [0, 8].
8
Now we can take out our constant: (1/2) * ∫ f(u) du = (1/2) * 18 = 9.
0
Notice that our new integral was our given value times (1/2). We can say this because even though we are no longer referring to the variable x, the function itself has not changed. We merely changed what we called the variable being plugged in, and it just so happened that the bounds on our new integral were the same as the original (the problem is purposely set up that way to help practice working with integrals and their properties).


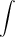 f(x)dx=18, find
f(x)dx=18, find 


