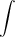The answer will be -A. Whenever the interval of integration is reversed, the resulting answer will be the opposite of that if we didn't switch the interval.
This can be more easily understood when thinking about what we are doing when calculating definite integrals. Our function that we are integrating has a resulting "potential function" if you will. When we evaluate the integral, we are simply subtracting the values of our potential function at two points (the points that define our interval. This means we have two numbers obtained from our potential function and we want to find the difference between them. Now we can use a simple property of subtraction to understand why flipping the interval gives us the opposite result.
If we define g(x) as ∫f(x)dx,
then ∫f(x)dx on the interval from b to a will result in g(a) - g(b).
We can now see from the example above that A = g(a) - g(b).
Now the ∫f(x)dx from a to b results in g(b) - g(a).
Notice that
g(b) - g(a) = - ( g(a) - g(b) ).
Substituting our value for g(a) - g(b) we get g(b) - g(a) = -(A).
Therefore, by flipping the interval of integration we obtain the opposite result from if we had not flipped them.