To approximate √99.4, we have to use formula for linear approximation as instructed, and it is:
f(x)≈ f(a)+f′(a)(x−a)
Since you are dealing with square root,
f(x)=√x
Therefore using derivative,
f'(x) = 1/(2√x)
Here, x=99.4 and I’m going to choose a =100 because that’s the closest perfect square number to 99.4. Therefore:
f(a) = f(100) = √100 = 10
f'(a) = f'(100) =1/(2√100) = 1/20
f(x)=f(99.4)≈ f(100)+f′(100)(99.4−100)
≈ 10+(1/20)(-0.6)
≈ 10+(1/20)(-0.6)
≈ 10 + (-0.03)
≈ 9.97


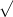 99.4
99.4


