VENN DIAGRAM URGENT !!!

Question

A Venn diagram is a common way for teachers and students to organize information. Have you ever seen a three-circle Venn diagram?

a) Create a Venn diagram by writing equations for three circles. Your equations do not have to create a perfect replica of this image, but your circles must overlap in a similar way. It may help you to visualize your equations if you graph them! What are the equations to your circles?

b) What are coordinates of the centers of your circles? Assign each center a name.

c)What is the distance between each pair of centers? Show how you arrived at your answer.

d) If you choose two of your circle equations and solve them, how many solutions will you find?

e)Now consider all three circles together. How many solutions would you find if you were to solve them all as one system? Explain how you know your answer is correct.

Answer 1

The equation of a circle is

(x-h)² + (y-k)² = r²

In this equation h is the x coordinate for the center of the circle and k is the y coordinate.

r is the radius of the circle.

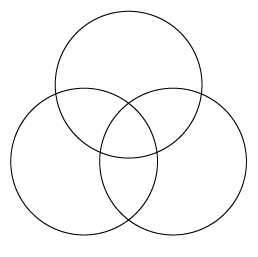
In a Venn diagram the centers of the circles are all the same distance apart.

You can imagine this as a triangle, and equilateral triangle.

If you were to write the coordinates for an equilateral triangle I would recommend by starting with two points either side of the y axis at (-1, 0) and (1, 0)

The third point will be a distance of 2 from each, since the first two points are 2 units apart.

To find this coordinate draw your equilateral triangle.

Your third point will be on the y axis.

Draw a line from your third point on the y axis straight down cutting the triangle in half.

Your job is to find the distance of the line you just drew.

You know the hypotenuse is 2 units and the base is 1 unit. So using the Pythagorean Theorem you can find the height of the side.

(Hint a² + 1² = 2² your answer will be irrational)

put that in the form (0, a) This is your third circle center. Name these yourself (A B C)

Lastly you need to determine the radius of the circles. If you sketch them out you will see that they look like the above diagram when the radius is around 2 units. But anything larger than that would also work.

Now you have all the information you need to write the functions of these circles.

The left one will be

(x - (-1))² + (y - 0)² = 2²

You can simplify it to

(x+1)² + y² = 4 Write the equations to the other circles using (1,0) and (0,a) as your centers and r = 2

c) You used the distance between centers to determine where the centers will be.

d) When determining the solutions to some equations on a graph the intersections will tell you where and how many solutions there are.

Looking at the Venn diagram in the problem, any two circles will have some intersections. Mark the number of intersections as the number of solution.

(This is not the total number of intersections in the diagram, but the number of intersections between only two circles)

e) The solution to all three equations will be a point where every equation intersects together.

(In the above diagram there is no point where each circle intersects. What does that say about the number of solutions?)

I understand that doing this without a drawing may be confusing so if you have any questions don't be afraid to comment.