If f and g are the functions whose graphs are shown, let u(x) = f(x)g(x) and v(x) = f(x)/g(x).

Question

If f and g are the functions whose graphs are shown, let u(x) = f(x)g(x) and v(x) = f(x)/g(x).

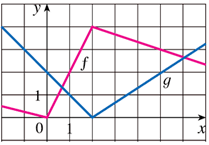
(a) Find u'(1).

=_______

(b) Find v'(5)

=_______

Answer 1

Since u(x) is a product of functions and v(x) is a quotient of functions, why not use the product rule to find u'(1) and the quotient rule to find v'(5)?

Answer 2

Because u(x) = f(x)g(x) then (by the product rule, u'(x) = f '(x)g(x) + f(x)g'(x)

Looking at the graph we see that:

f(1) = 2

f '(1) = 2

g(1) = 1

g'(1) = -1

So u'(1) = (2)(1) + (2)(-1) = 2 - 2 = 0

Apply the same logic for v(x). Since v(x) = f(x)/g(x) then v'(x) = [f '(x)g(x) - f(x)g'(x)]/(g(x))²

f(5) = 3

f '(5) = -1/3

g(5) = 2

g'(5) = 1/3

So v'(5) = [(-1/3)(2) - (3)(1/3)]/(2)² = (-5/3)/4 = -5/12