
Nitin P. answered • 06/25/20
Machine Learning Engineer - UC Berkeley CS+Math Grad
We start with the indicated substitution and find dx. We have:
x = 4sec(z)
z = sec-1(x/4)
dx = 4sec(z)tan(z)dz
Then, we have:
∫sqrt(x2 - 16)dx/x = 16 ∫sqrt(sec2z - 1)sec(z)tan(z)dz/[4sec(z)] = 4 ∫sqrt(sec2z - 1)tan(z)dz = 4 ∫tan2z dz
Now, we have:
4 ∫ tan2z dz = 4 ∫ (sec2z - 1)dz = 4(tan z - z) + C = 4tan(sec-1(x/4)) - 4sec-1(x/4) + C
Simplify the nested trig function by setting up a triangle. The hypotenuse is x and the adjacent side is 4, so the opposite side is sqrt(x2 - 16). Therefore, our final answer is:
∫sqrt(x2 - 16)dx/x = = 4sqrt(x2 - 16)/x - 4 sec-1(x/4) + C


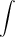
 x
x

