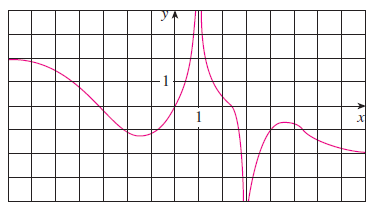
Jonathan C. answered • 06/23/20
Experienced High School Math Teacher and Tutor
a) Look at the part of the curve that is closest to infinity. It would be the part of the curve furthest to the right. As the values of x increase, the values of y are going towards -2. Therefore the answer is -2.
b) Look at the part of the curve that is closest to negative infinity. It would be the part of the curve furthest to the left. As the values of x get smaller (you are moving left along the number line), the height of the curve is going towards 2. Therefore the answer is 2.
c) At x = 1, the function is not continuous (there is a break in the graph), we must evaluate the limit from the left and right sides. As x approaches 1 from the left (from the negative side), the y-values of the function are going towards infinity. As x approaches 1 from the right (from the positive side), the y-values of the function are going towards infinity. Since both left and right limits are going to infinity, your limit is infinity. You can also say that the limit does not exist.
d) At x = 3, the function is not continuous (there is a break in the graph), we must evaluate the limit from the left and right sides. As x approaches 3 from the left (from the negative side), the y-values of the function are going towards negative infinity. As x approaches 3 from the right (from the positive side), the y-values of the function are going towards negative infinity. Since both left and right limits are going towards negative infinity, your limit is negative infinity. You can also say that the limit does not exist.
e) Vertical asymptotes occur where the y values of your function go to infinity or negative infinity. This occurs at x = 1 and x = 3 (This is what we showed in parts c and d).
Horizontal asymptotes occur if the limit of the function as x goes to + or - infinity equals a constant. This was done in parts a and b of this question. The horizontal asymptotes are y=-2 and y = 2.