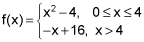Iftekhar A. answered • 01/08/20
Computer Science Tutor from UC Davis With Industry Experience
Before we get into this problem, let's review the basics of how to find the absolute maximum of a function. To find the absolute maximum, we need to test the end points and critical points. The highest value we get by plugging in the above-mentioned points will be the absolute maximum.
Now let's write the two functions in the piece-wise function separately.
y1 = x^2-4 on the interval [0,4] and y2 = -x + 16 on the interval x>4
Before doing any calculations, we can predict that maximum value will probably not be in the second function since it is a downward sloping straight line. Meaning that every value of x will just give us a smaller and smaller value of y. Now, let's get into the math.
First, let's test the end points. By plugging in 0 and 4 into y1, we get -4 and 12 respectively. Now, we need to find any critical points. We can do this finding the derivative, which gives us 2x, and setting it to 0. This gives a critical point at x = 0.
We know that x = 0 is a minimum value, since it is a quadratic equation with a positive coefficient of x^2. However, we can show that mathematically too. If you want to skip this part, you can go ahead to the next paragraph. To see if x = 0 is a relative max or min, we need to text points before and after it. If we plug in a value before 0, say -1, into our derivative, we get a negative answer. If we plug in a value after 0, say 1, we get a positive answer. Since the function's slope is going from positive to negative at x=0, we can understand that x = 0 is a minimum.
Since x = 0 is a minimum, we don't need to test it as we are interested in only the maximum. Therefore, the only points we are concerned about, it seems, are the end points which are -4 and 12. Since 12 is the larger number, 12 is our absolute maximum.
Hope I was able to help! Feel free to reach out with any questions.