Using Euler's Method?

Question

Using Euler's Method with a step size of h = 0.5, estimate the value for y(3) for the differential equation 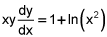 , with y(2) = 5.

Answer 1

y(2) = 5 means x=2 when y=5 and vice versa.

(2)(5)(dy/dx) = 1 + ln(2^2)

10 (dy/dx) = 1 + ln(4)

dy/dx = (1 + ln4)/10 is the slope of the line...

the intercept B = y - mx

= 5 - 2* (1 + ln4)/10

= (50 - 2 - 2*ln4)/10

= (48 - ln 8)/10

So the linear equation for this step is:

(1 + ln4)x/10 + (48 - ln 8)/10

Next x=2.5

Then y1= [(1 + ln4)*2.5 + (48-ln8)]/10

= [ 2.5 + 2.5 ln 4 + 48 - ln 8]/10

= [ 50.5 + 2.5 ln 4 - ln 8]/10

So the point is (2.5 , y1)

You then plug this point into the differential equation to

get the slope for the next line. Use this same point

to find it's intercept.

Finally plugs x=3 into the new line to get the approximation.

The following table summarizes the approximation, but

with a step size of h=0.1.

2 5

2.1 5.02386294361119891

2.2 5.04740652918363154

2.3 5.07061299900701384

2.4 5.09347120986780908

2.5 5.11597499757106115

2.6 5.13812195071366369

2.7 5.15991248428259021

2.8 5.18134913515256811

2.9 5.20243602332564949

3 5.22317843799946621

As R Bruce N. suggests, the D.E can be solved by separation.

Multiplying both sides by dx/x

y dy = (1 + ln(x^2))*dx/x

= (1 + 2*lnx)*dx/x

Integration:

U = 1 + 2*lnx

dU = 2 * dx/x

(1/2)dU = dx/x

y dy = (1/2) U * dU

y^2 = (1/4) U^2 + c

y = sqrt( (1/4)U^2 + c)

Applying the initial condition:

5 = sqrt( 1 + c)

25 = 1+c

c=24

y = sqrt( (1/4)(1 + 2*lnx)^2 + 24)

At x=3, the exact value is 4.979890173922920445684+