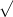Differentiate the function

Question

Differentiate the function.

y = 2x log6

x

Answer 1

if the problem is y = (2x)log₆(x) Then y/2x = log₆₍x) and 6^(y/2x) = x

Now, take the natural log of both sides to get (y/2x)ln6 = ln(x) Then y = (2x/ln6)ln(x)

Taking the derivative, we get y' = (2/ln6)ln(x) + (2x/ln6)(1/x) = (2/ln6)ln(x) + (2/ln6) = (2/ln6)(1 + ln(x))