Discuss the Discontinuity

Question

Discuss the Discontinuity of 

f(x) = x+7/x^2-49

non-removable and removable

 

Answer 1

Hi!

Happy Easter!

There is classification of discontinuities (you have at x=0 the Type 3)

 

1. The one-sided limitfrom the negative direction

   

   and the one-sided limit from the positive direction

   

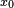   at exist, are finite, and are equal to . Then, if ƒ(x₀) is not equal to , x₀ is called a removable discontinuity. This discontinuity can be 'removed to make ƒ continuous at x₀', or more precisely, the function

   

   is continuous at x=x₀.
2. The limits and exist and are finite, but not equal. Then, x₀ is called a jump discontinuity or step discontinuity. For this type of discontinuity, the function ƒ may have any value in x₀.
3. One or both of the limits and does not exist or is infinite. Then, x₀ is called an essential discontinuity, or infinite discontinuity. (This is distinct from the term essential singularity which is often used when studying functions of complex variables.)

+++ IHM

1. The one-sided limitfrom the negative direction

   

   and the one-sided limit from the positive direction

   

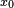   at exist, are finite, and are equal to . Then, if ƒ(x₀) is not equal to , x₀ is called a removable discontinuity. This discontinuity can be 'removed to make ƒ continuous at x₀', or more precisely, the function

   

   is continuous at x=x₀.
2. The limits and exist and are finite, but not equal. Then, x₀ is called a jump discontinuity or step discontinuity. For this type of discontinuity, the function ƒ may have any value in x₀.
3. One or both of the limits and does not exist or is infinite. Then, x₀ is called an essential discontinuity, or infinite discontinuity. (This is distinct from the term essential singularity which is often used when studying functions of complex variables.)

Answer 2

The function as presented was:

f(x) = x+7/x^2-49

Technically, previous answers have treated the original function as:

f(x) = (x+7) / (x^2-49)

note that the order of operations would be different, with the added parentheses. If we go with the originally written function, the division that creates a discontinuity would be 7/x^2; and the zero divisor that creates a discontinuity is when x^2 = 0, which reduces to x = 0. As 7 is a non-zero numerator, that would lead to a non-removable discontinuity.

Answer 3

Discontinuities in functions are apparent "holes" in a function where no output value (f(x) also known as y) exists for a particular input value (x).
In problems like yours, where there is a polynomial in the numerator (x + 7) and another polynomial in the denominator (x^2 - 49), it is usually best to first factor these polynomials:

(x + 7) / (x^2 - 49) = (x + 7) / [(x + 7)(x - 7)]

Then find the discontinuities by setting each of the factors in the denominator to a value of 0 and solving for x:

x + 7 = 0 , x - 7 = 0

Your particular problem has two discontinuities:

x = 7 and x = -7

Both of these values create discontinuities because they cause the function to divide by zero.

Here's a QUICK-AND-DIRTY method for determining whether a particular discontinuity is REMOVABLE or NON-REMOVABLE:
If the discontinuity is caused by a division by zero, check to see if the numerator is also zero when you plug in the x-value for your discontinuity. If the numerator is any value besides zero, the discontinuity is probably NON-REMOVABLE; if the numerator is zero, the discontinuity is probably REMOVABLE:

[(7) + 7] / { [(7) + 7] [(7) - 7] }
= [14] / { [14] [0] }
= 14 / 0
NON-REMOVABLE

[(-7) + 7] / { [(-7) + 7] [(-7) - 7] }
= [0] / { [0] [-14] }
= 0 / 0
REMOVABLE

With this type of function (polynomial / polynomial) REMOVABLE DISCONTINUITIES are usually just a MISSING POINT in the graph of the function; whereas NON-REMOVABLE DISCONTINUITIES are usually VERTICAL ASYMPTOTES.

In future problems, be sure to check for any square-roots in the function. These can cause their own discontinuities when they take the square-root of a negative value. These discontinuities don't always follow the QUICK-AND-DIRTY method I showed you. Instead of causing a MISSING POINT, or just a VERTICAL ASYMPTOTE, square-roots usually cause VERTICAL ASYMPTOTE where on one side the function exists on to infinity, and the other side doesn't exist on toward infinity in the opposite direction. These are almost always NON-REMOVABLE discontinuities.

Answer 4

SEE OTHER ANSWER. IT IS MORE COMPLETE.

 

A discontinuity occurs when the function does not have an answer at a certain point. Usually this is caused by one of two things: division by zero or taking the square root of a negative number.

Here, f(7) creates a discontinuity, because the denominator becomes (7)^2 - 49 = 0, and division by zero is not possible.

Factoring the denominator to read (x+7)/[(x+7)(x-7)] lets us simplify the equation to be 1/(x-7), but unfortunately this does NOT remove the discontinuity. If the numerator had read (x-7) as opposed to (x+7), we would have been able to end up with 1/(x+7), and we would no longer have the discontinuity.

Visualising this discontinuity is easy. Simply substitute in numbers that gradually approach 7, first 'from the left' (as in, going from 6 to 7), then 'from the right' (going from 8 to 7). From the left, the numerator is positive, but the denominator is negative, as (6.99999)^2 < 49. You are dividing by ever smaller negative numbers, thus, f(x) approaches NEGATIVE infinity. From the right, (7.0000001)^2 > 49, so it is always positive as it approaches zero, thus, f(x) approaches positive infinity.
 

When this happens, we call it a vertical asymptote, and it occurs at f(7)