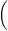Alright, I'm going to simplify those equations as the function doesn't do it justice.
Maximize P = 3.5x + 3y
Constraint 1: 5x + 3y ≤ 30
Constraint 2: 2x + 3y ≤ 21
Constraint 3 (and 5): 0 ≤ x ≤ 4
Constraint 4: y ≥ 0
a) Alright, so this is going to be a graph in the first quadrant where we have slant lines along those first 2 constraints. Pretty much you'll be looking for corner points and then determining which point is the maximum. I like to look at x and y intercepts and just pick the smallest one.
x-intercepts
1) x=6, 2) x=10.5, 3) x=4. So (4,0) is a corner point.
y-intercepts
1) y=10, 2) y=7. So (0,7) is a corner point.
So those first two will intersect, likely before x=4, so let's see where that is.
Subtract 2 from 1: 3x = 9, x=3. So the corner point is (3,5)
This means that there will also be a corner point at x=4. Since the first constraint has a bigger slope, we'll just plug in x=4 into that equation and solve for y: This gives the corner point (4,10/3).
Finally, plug these values into P and find the maximum.
(4,0): P=14
(0,7): P=21
(3,5): P=25.5
(4,10/3): P=24.
x=3 and y=5 maximizes P at 25.5.
b) So for this I'll first sub in c for the x coefficient and find the values of P.
(4,0): P=4c
(0,7): P=21
(3,5): P=3c+15
(4,10/3): P=4c+10
For it to not change the conditions 3c+15 must be the max. Comparing this to the second point, we know that c>2. Comparing this to the fourth point, we know that c<5. So the range that doesn't change the optimum solution is 2<c<5.
c) For this one, just solve for x or y equal to 0. This gives 10 and 6 respectively. But based on the rest of the conditions, the maximum x+y can equal is 8 from the 3rd point. So resource 1 must be between 6 and 10 (or 8 if the other Resources are needed to be seen) of the x,y components.
d, e) I'm not sure on these concepts as they are more economic ideas, so I'll defer to those with more understanding of those concepts.