
Yefim S. answered • 10/25/22
Tutor
5
(20)
Math Tutor with Experience
g(2.99) = g(3) + g'(3)(2.99 - 3) = 3 + 3(- 0.01) = 2.97
g(3.2) = 9(3) + g'(3)(3.2 - 3) = 3 + 3(0.2) = 3.6
Hey H.
asked • 10/14/22Use differentials and the graph of g' to approximate g(2.99) and g(3.2) given that g(3) = 3.
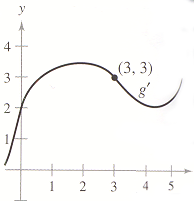
g(2.99) ≈
g(3.2)=

Yefim S. answered • 10/25/22
Math Tutor with Experience
g(2.99) = g(3) + g'(3)(2.99 - 3) = 3 + 3(- 0.01) = 2.97
g(3.2) = 9(3) + g'(3)(3.2 - 3) = 3 + 3(0.2) = 3.6
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.