Question included in description

Question

Minimizing Construction Costs

 The management of the UNICO department store has decided to enclose a 911 ft²area outside the building for displaying potted plants and flowers. One side will be formed by the external wall of the store, two sides will be constructed of pine boards, and the fourth side will be made of galvanized steel fencing. If the pine board fencing costs $7/running foot and the steel fencing costs $2/running foot, determine the dimensions of the enclosure that can be erected at minimum cost. (Round your answers to one decimal place.)

There is a rectangular fence enclosing space outside of a building. The rectangle is formed by the external wall of the building, one side of galvanized steel fencing, and two sides of pine wood boards.

wood side ft

steel side 

 ft

Answer 1

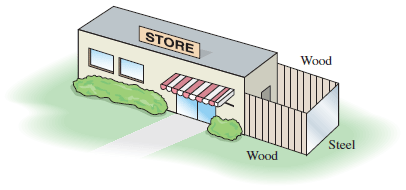
I find the picture confusing because it looks like the side covered by steel is supposed to be as long as the side of the building.

So instead I will assume that the side of the building is actually longer than any potential length of the steel fencing.

Let

p be the length of each of the sides where pine fencing is to be used,

s be the length of the side where steel fencing is to be used.

The cost of the fencing is then

c2(p, s) = 7p + 7p + 2s

We have the constraint that ps = 911, i.e.

s = 911/p

Therefore we can express the cost in term of p alone

c(p) = 14p + 1822/p

Minimum cost will be achieved for the value of p where the derivative of c'(p) = 0.

c'(p) = 14 - 1822/p²

Setting it to zero, and calculating the optimal p

14 - 1822/p² = 0

p = √(1822/14) = 11.4 ft

s = 911/11.4 = 79.9 ft