Find the sum of the infinite series whose sequence of partial sums, Sn, is

Question

Find the sum of the infinite series whose sequence of partial sums, S_n, is 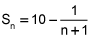 . (4 points)

	10
	0
	9.99
	Sum does not exist

Answer 1

Hello!

So, keep in mind that what we mean S_n. It is what we get after adding together the first n terms of some sequence a_n. So, for example, if we had a sequence of terms that we wanted to add together, let's say it's a_n=1 (that is, every member of the sequence is 1), we can find it's sequence of partial sums S_n. To list a few, S₁ = 1, S₂= 1+1, S₃=1+1+1, and so on. You'd see that S_n = n. So if we wanted to find the infinite sum of a_n, we would take the limit of S_n. (In this example case, we'd be doing lim_n->∞n, and since this limit doesn't exist, we say the infinite series does not converge, or diverges...in other words, if you add 1+1+1+1+1...forever, it does not converge to any value: quite intuitive!).

Now, back to your problem! If your partial sums are given by S_n= 10 - 1/(n+1), then all we want to do is take the limit of S_n.

Therefore your answer is:

lim_n-->∞S_n = lim_n-->∞(10 - 1/(n+1)).

= lim_n-->∞10 - lim_n-->∞(1/(n+1))

=10 -0

=10.