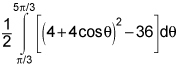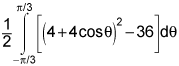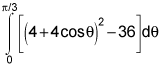Which one or ones of the following integrals produces the area that lies inside the cardioid r = 4 + 4 cos θ and outside the circle r = 6?

Question

Which one or ones of the following integrals produces the area that lies inside the cardioid r = 4 + 4 cos θ and outside the circle r = 6? (5 points)

1. 
2. 
3. 

answer choices

	I only
	II only
	II and III only
	I and IIII only

Answer 1

This question is entirely conceptual and requires you to understand the relationship of enclosure with 2 shapes, properties of integration, and how to find critical points.

First of all, we must understand the question. It helps to visualize what the enclosure might look like and where it takes place on the cardioid and circle. You can use some graphing calculator to help you visualize if you need. I'd recommend desmos.com. The integration is dependent on the difference in r so therefore the enclosure is the difference between them. What that tells us is that we need to set the r's to be equal to one another. 4+4cosθ = 6 or if we simplify this, arccos(1/2) = θ and solve for all applicable theta. These will be our critical points.

Once you've done this (using your knowledge of the unit circle) we can say that the bounds of integration are from theta A to theta B or theta B to theta A. But we can only know which one it is by re-reading the question. The enclosed region is defined by being outside the circle but within the cardioid. This tells us with a simple inequality that 4+4cosθ > 6 for the entirety of our interval. When you determine this, you can now set up your integral of the area of the cardioid to be

A = 1/2 ∫f(x)² -g(x)² dθ where the bounds of integration will end up being in a clockwise manner. If you do it the other way, your Area would appear to be negative but we know that to be impossible so it would cause no issues.

All areas of regions bounded by a polar curve have the 1/2 out in front due to the nature of finding the area of a polar sector.

Once you have found the proper integral set up, consider that the area of a semicircle is exactly half of that of a full circle. Thus, we could rewrite the integral to be multiplied by 2 but integrated over half of the area we were determining before because those corresponding regions are symmetrical.

The answer should include two of the provided integral options.