Find the equation of the curve that passes through the point (x, y) = (0, 0) and has an arc length on the interval given by the integral

Question

 

Find the equation of the curve that passes through the point (x, y) = (0, 0) and has an arc length on the interval 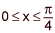 given by the integral  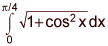. (5 points)

answer choices

	y = sin(x)
	y = cos(x)
	y = cos-1(x)
	y = tan(x)

Answer 1

Hi Stephanie B.,

Perhaps you were as puzzled as I was by the odd phrasing, "has an arc length on the interval". if it means, a total arc length from x=0 to x=π/4, then I guess you could pick the appropriate function from the offered set by considering the argument in the given integral. Consider a small interval, dx. The function you want must have a slope, such that the hypotenuse of the resulting right triangle tangent to your function curve has the form (1+cos²(x))^0.5 dx. Now work backwards from the Pythagorean theorem to your original function. If f ' (x) = cos(x), what was f(x)? (You know this from your trig derivatives??)

BUT --- is this answer unique? No, if you take the information as noted above -- it's just any function that happens to have that arc length over that total interval. Perhaps what the questioner MEANT to ask was for the integral over the interval from 0 to x. That would "lock in" the answer uniquely. Except for the obvious possibility of the negative of that function -- obviously has the same arc length characteristics!

-- Cheers, --Mr. d.