
Giorgio C. answered • 11/10/20
PhD Aerospace Engineering: Algebra, Calculus, Matlab, Geometry,Italian
dy/dx = (dy/dt)*(dt/dx)
dx/dt = (3t^2 + 12*t + 9) --> dt/dx = 1/ (3t^2 + 12*t + 9), where you have to exclude the values of t that make the denominator equal to zero.
dy/dt = 6*t^2 + 18t - 24 = 6(t^2 +3t -4) = 6(t+4)(t-1), which is equal to zero when t = -4 or when t = +1.
since dy/dx = (dy/dt)*(dt/dx), where dt/dx cannot be equal to zero, and dy/dt equals zero for t = -4 and t = 1; then dy/dx = 0 when dy/dt = 0.


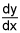 = 0 for the parametric equations x = t
= 0 for the parametric equations x = t

